Bow Statics & Kinematics: Carbon-Fiber vs. Pernambuco

[graph above is from Ulrike Wegst (Am J Botany 2006; 93:1439-48) who is now at Drexel Univ in Philly. In the blogpost below, roll-over 'alt-text' shows attributions of items reproduced from others' work, as well as results from my own measurements. DSM.]

I    wonder if you could shed some light on differences between pernambuco and carbon-fiber bows. Are there physics reasons why they should play or sound different?
  —  Anonymous email to CMT blog.

A ctually, yes. It’s been a subject of active interest and research for several academic acoustics teams for at least 20 years, probably longer. And there are several bowstick patents that have issued in recent years, which identify specific physical properties of the polymer carbon-fiber composite and the bowstick design as a basis for the bows’ proprietary advantages in terms of acoustics and playability.

Property	Carbon Fibre	Pernambuco
Density, ρ (gm/cm3)	1.50 – 1.80	1.06 – 1.22
Speed of sound, c (km/sec)	6.3 – 22	5.0 – 5.9
Young’s modulus, E (GPa)	7.4 – 150	5.0 – 22
Equation (my own regression)	c = 0.02573 +  1.1435 (E/ρ)0.5	c = 0.08160 +  1.1896 (E/ρ)0.5
Acoustic impedance, Z (N•sec/m3 or MPa•sec/m)	3.3 – 40	2.3 – 7.2
Coefficient of sound radiation, R	1.5 – 12.2	2.0 – 4.8

I  myself found the different weight distribution of the bow along its length to be dramatically different between pernambuco and carbon-fiber, when I performed measurements on my own violin bows. The force applied by the weight of the right hand on the bow (and transmitted by the hand from the arm, etc.)—the forces are surprisingly different between the bows. The carbon-fiber generally has a higher elasticity and higher Young’s modulus (elastic modulus), compared to the pernambuco. Carbon-fiber-polymer composite’s stiffer and gives clearer tactile feedback, which enhances subtle, technical timing in bowing. You do not have to be an accomplished or professional string player to be able to perceive this when you play...

I t is, as you know, quite difficult to produce a constant volume of sound (with constant speed), for this result requires a non-constant amount of pressure so as to compensate for the changes in the weight of the bow. Even a beginner can feel this. So it takes some getting used to—switching to a bow of totally different material and design, with different weight and stiffness distributions along the bowstick’s length.

T he ‘ballistic’ effects of the bow’s motion have been extensively studied, but there is still a lot that is not adequately understood, and this CMT post will not go into dynamics/ballistics. It’s enough, though, just to look at the ‘statics’ and ‘kinematics’, as physicists and mechanical engineers refer to it—which is what this CMT post is about.

S o, in response to the reader’s email question above, I performed a series of measurements on my own two bowsticks—not a sample that is statistically generalizable, admittedly, but interesting/provocative as an illustration nonetheless.

M odern wood bowsticks are predominantly between 25 gm and 35 gm for the stick alone, without fittings or hair, etc. Then you add 6 gm of bowhair. The frog and screw and fittings bring the total weight up somewhere between 55 and 67 gm. Both of my bowsticks measure exactly 75 cm in length and both weigh exactly 61 gm total.

F or carbon-fiber bowsticks made according to the Glasser patent '353 , the bowstick shaft and head have a solid core of polyurethane foam and are wrapped with unidirectional carbon fibers running along the longitudinal axis of the shaft. Some companies inject a carbon mixture into the mold rather than wrapping. (The mixture is either completely dry, partially impregnated with resin, or totally impregnated with plastic resin.) These resins are epoxies or other ‘thermosetting’ plastics, meaning they cure to a hard solid when heated and can’t revert to their previous melt-y, liquid state when heated again. The assembly (called the ‘preform’ or ‘pre-preg’) is placed into a mold and the mold is closed about the perform. Glasser and other use a ‘resin transfer molding’ to infuse resin under pressure into the mold when the mold is closed. The mold is heated until the ingredients solidify or ‘set’. The whole thing is baked to cure the resin and make a nice, hard bowstick. Subsequently, the mold is opened, the stick is machined and finished and fitted out with hair and hardware.

I n any case, remember that the carbon-fiber bowstick is a ‘composite’ a molded ‘laminate’ comprised of various layers, usually around a cylindrical ‘core’, plus infused plastic. It is not a solid ‘lump’ of one thing called carbon-fiber. It is a complex, laminated ‘composite’. The longitudinal acoustic properties of the thing may be dominated by the outer plastic-carbon-fiber layers and the density and Young’s modulus of those layers. But the transverse and bending stiffness and other properties—overall, or at any point along the length of the bowstick—are not constant along the length and are strongly influenced by all of the materials that are present in the cross-section of the composite laminated structure at each point. The stresses are not constant either. They vary between and across the layers in cross-section...


W hen I got my JonPaul Avanti™ bow, right away I noticed subtle differences in clarity, fullness of sound, surface noise, and so on.


B oth of my bows are easy-playing, but the JonPaul one has a firmness throughout (at tip, middle, and frog) and seems much more ‘forgiving’. It is able to play more delicately and yet, paradoxically, it is also somewhat louder-playing than my pernambuco bow. The JonPaul has easy balance and emits a tone that forgives many of my misjudgments. The bowhair surface noise (frequencies from about 5KHz to 10KHz) is pleasant and has a somewhat ‘nicer’ personality than that of my other bow. The carbon-fiber bow feels, for some reason, “lighter” than the pernambuco one. If I want to apply more exuberant force I can do that. But the inherent pressure of the carbon-fiber bowstick and its bowhair on the string is less—several grams less for the carbon-fiber bow compared to the pernambuco bow—throughout the bowstroke.

T he firmness and flexibility were far different than my pernambuco bow, even though both of them weigh 61 gm and both of them are exactly 75 cm long. The balance and stability of the two bows are totally different. The center-of-gravity of the JonPaul is 24.5 cm from the screw-end of the bow, while the pernambuco one has its center-of-gravity a whole 3 cm closer to the midpoint of the bow.

I  made a simple spreadsheet to explore the ‘statics’—how the force and balance of the two bows compare, as a function what part of the bow I am using. You can click on the screen-shot below to download a copy of the Excel sheet and play with it yourself if you like. Slide the slider leftward and rightward to see how big the difference is in grams of force at various positions of the bow on the string...

I    t is generally agreed among musicians that the quality of a bow can be rated in two areas, dealing with; (1) the way the bow can be controlled in playing (‘playing properties’), and (2) the influence of the bow on the tone quality (‘tonal properties’). It seems reasonable to assume that both of these quality aspects are basically defined by the mass and stiffness distributions along the bowstick.
  —  Anders Askenfelt, KTH, Stockholm, 1995.

I    suggest trying something that costs, say, at least half as much again as the most that you think you might be prepared to pay, just to have an insight into what the difference would be for you to go to the ‘next level’. You will know a good bow when you know you are playing with something that really feels that it’s ‘lifting’ the style of your playing.
  —  Anonymous, teachers’ online forums, Associated Board of the Royal Schools of Music, 18-JUN-2007.

T he up-shot of my measurements and this simple statics/kinematics analysis is that (a) having the lighter, hollow tip on the JonPaul and (b) having the center-of-gravity 3 cm closer to the frog do make the ‘default’ inherent carbon-fiber bow’s pressure on the string several grams force less than the pernambuco of the same length and weight (see the plot in the screenshot, BROWN for carbon-fiber and BLUE for pernambuco) throughout the bowstroke. It ‘feels’ lighter than the pernambuco, even though the two weigh the same 61 gm and even though the carbon-fiber composite in the JonPaul is more dense than the pernambuco on a gm/cm³ basis. This seems counter-intuitive to me.

S o surprising, in fact, that I decided to do some deflection-vs-pressure measurements to shed further light on what’s going on. Here are two plots, which show that the carbon-fiber curves are left-shifted and have a smaller slope. The red-dot shows where the center-of-gravity is.


I  am betting the paradoxical ‘louder-and-yet-more-delicate’ quality of the carbon-fiber bow is due to the higher sound radiation coefficient, R (also called ‘modulus of flexural rigidity’, equal to c/ρ), or, more accurately, R in combination with a slightly higher ‘loss-tangent’ for the carbon-fiber in the JonPaul bow compared to the pernambuco bow. The loss-tangent tan(δ) is a parameter that measures the degree to which a material internally damps or dissipates vibrational energy. Maximizing the ratio of the stiffness-per-unit-weight to the loss-tangent is what gets you peak sound intensity and responsiveness—it’s how they choose materials for piano soundboards, violin top plates, high-performance loudspeaker cones, stage and concert-hall floors and wall coverings, all sorts of things. Have a look at Bartlett’s 1997 paper if you’re interested in how R affects sound.


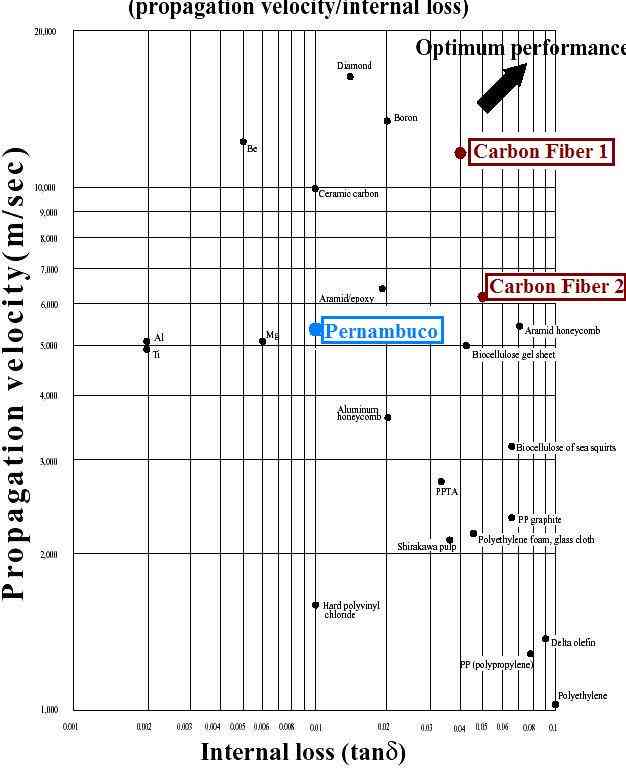
T he product ρ*c is called the acoustic impedance, Z. That, too, is far higher for the carbon-fiber compared to the pernambuco. See the nice 2006 paper by Ulrike Wegst (Max-Plank-Institut, Stuttgart; Lawrence Berkeley National Lab, Berkeley, CA) for more info on this. The efficient propagation (transmission and reflection) of acoustic energy from the slipping-sticking bowhair to and through the bowstick undoubtedly has a role. Evidently, the higher Z is, the better. I hope John McLennan’s group at Univ New South Wales or some other acoustical physics team studies this sometime...

I n polyethylene and other soft plastics (ones not suitable for bowsticks), sound velocity decreases significantly with increasing stick length. This is not as pronounced in hard thermosetting plastics like carbon fiber epoxy composites used for bowsticks. We do not expect noticeable differences in c caused by a length difference of a few centimeters between two bowsticks made of the same material...


I n polyethylene, there is a also nearly-linear relationship between sound velocity and density. But in pernambuco and carbon fiber composites and other ‘hard’ materials, c is approximately proportional to the square root of Young’s modulus divided by the density. I performed some statistical regressions of this from available published data, just to confirm the quantitative mathematical relationships between these quantities. (The regression coefficients I got are in the Table up at the top of this post.)

   E ~ K₁*ρ*c² or

   c ~ K₂*(E/ρ)^0.5


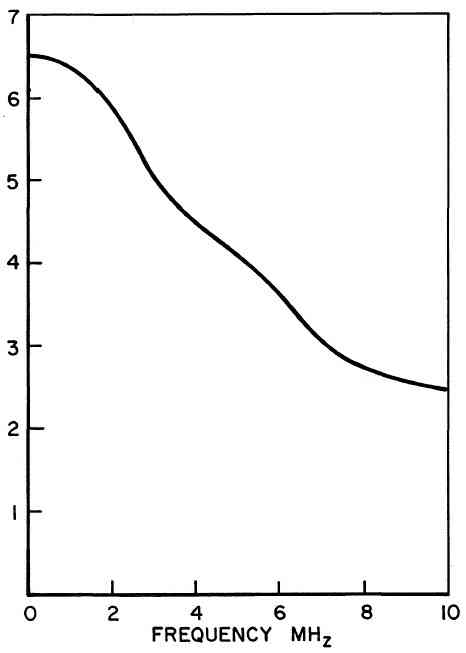
E  and c are, of course, not strictly constant; they depend on frequency ω (wavelength), especially when the dimensions of the stick are comparable to the wavelengths of the [high-frequency] sounds.

   c(ω) ~ c₀*(1 – K₃*ω²) [left-hand portion of Figure above, anyway].

B ut the frequency effects are very small until you get up into the ultrasonic range of frequencies, so, for violin bows and music of normal tessitura, we can assume c is constant, to a good approximation.


Y oung’s modulus, E, is measured in two ways: by mechanical bending and tension measurement, and by measuring the velocity of sound in the material. Interestingly, the two measurement methods don’t necessarily yield the same answer. The velocity measurement gives an E value that is up to about three times larger than values obtained from the bending and tensile tests in polyethylene. In wood and carbon-fiber composites, the difference is usually not so big—generally, the mechanical and acoustic values for E agree within about 50% (see Mann 1979). Why? For sonic stress-wave propagation, the displacements (strain) are microscopic—micrometers at most—whereas, for mechanical bending and tension, the displacements are at least three orders of magnitude bigger, millimeter-size in typical test-objects. The high sonic and ultrasonic frequencies used for acoustic determinations of E afford little time for ‘creep’ or other time-dependent effects to be manifested.

Y oung’s modulus obtained from sound velocity measurements can be plotted as a function of density and compared with Young’s modulus measured by bending and tensile tests. Some of the references below (links at bottom of this post) do this...

M aybe the most obvious discrepancy between mechanical and sonic measurements is seen as different dependencies on moisture content. The mechanical moduli decrease exponentially as moisture content of wood or plastic increases. Sonic data indicate that the acoustic Young’s modulus does not decrease nearly as fast as a function of percent moisture content. Maybe virtuosic performers can tell the difference between a humid bowstick and a very dry bowstick. But the opportunity to assess this almost never arises. The other variables (effect of humidity on bowhair, on instrument, etc.) would be far larger than the effect on just the bowstick. So assume c and E are constant in any particular bowstick...

M ost bow making and materials science literature neglects the fact that Young’s modulus is not a constant, fixed number. But Young’s modulus is the slope of the stress-strain curve. This curve is not necessarily a straight line; in fact, usually only portions of the curve are somewhat straight. It has bends and shoulders in it. The slope is not constant. And some materials are more non-linear than others. Polymers’ Young’s modulus values are especially curvy—they increase by up to 30% as strain increases, because of changes in molecular alignment of the polymer chains as the plastic is put under more stress and stretches. Would this influence the difference between the carbon-fiber bow and pernambuco bow sounds?

C arbon fiber can increase in modulus by 25% from zero strain to ultimate strain. Composite materials do change in modulus as fiber alignment changes due to strain. The fact that the speed of sound can increase with increasing stress is used in aerospace industry to accurately measure and QA the torque that’s applied to bolts and other fasteners in airplanes and spacecraft. An ultrasonic signal to measure the speed of sound in a torqued bolt is compared with a non-torqued control fastener. But the few Newtons of force generated by a violin bow screw tightening the bowhair are not enough to change E or c by even 1%. So assume these properties are constant, in any bow engineering or experiments we do...

C arbon fiber bows are, in general, more durable than pernambuco bows. They’re fairly impervious to humidity and temperature changes, so they resist warping. And they’re priced economically (especially when compared with wooden ones that deliver similar acoustics and mechanics).

F inally and not insignificantly, carbon-fiber bows are comparatively ‘green’ environmentally (see Baillie 2005), compared to pernambuco harvested in tropical rainforest South America.

B    y the end of the eighteenth century, the once common [pernambuco tree (Pau-brasil, Caesalpinia echinata) ] had become a rare species in the state of Pernambuco and, soon thereafter, the rest of its natural habitat. By the end of the twentieth century, it has been virtually extirpated from its range and is currently registered on the IUCN World List of Threatened Trees. It is not, however, list on Appendix I or II of the Convention on the International Trade of Endangered Species (CITES) and was not officially recognized as being in danger of extinction and protect under Brazilian law until 1990. Trade in pernambuco continues to contribute to deforestation of the Atlantic rain forest and its eventual disappearance as a commercial species.
  —  Yurij Bihun, Woodwork, 2000.

T hanks for the question! I had fun exploring some of the reasons why my own wood and carbon-fiber bows are so different. I feel that I now have a better understanding of what makes my own bows behave as they do. And I hope some of the things above and the links below are useful to you as well.

• Anders Askenfelt page at KTH Stockholm
  
• Ulrike Wegst page at Drexel Univ Dept of Mat Sci and Eng
  
• MIL-STD-17-1F. Composite Materials Handbook. U.S. DoD, 2002. [4.4MB pdf]
  
• iMechanica.org
  
• Pernambuco page at ArcosBrasil.com
  
• Pernambuco regulations discussion on MaestroNet.com
  
• JonPaulBows.com
  
• International Pernambuco Conservation Initiative (IPCI-USA.org)
  
• Violin Society of America (Intl Violin & Bow Making Competition)
  
• British Violin Making Association
  
• ArcusBow.de (Bernd Müsing, Andreas Wetzlinger, et al.)
  
• Lucchi time-of-flight acoustic velocity meter
  
• BowWorks.com
  
• MatWeb.com property search
  
• Violin Bows page at Univ New South Wales Physics Dept.
  
• John McLennan page at Univ New South Wales Physics Dept.
  
• PhysClips at Univ New South Wales
  
• Arnold V. Mathematical Methods of Classical Mechanics. 2e. Springer, 1997.
  
• Askenfelt A. Observations on the violin bow and interaction with the string. KTH report, 1995. [1MB pdf]
  
• Askenfelt A. Measurement of bow motion and bow force in violin playing. J Acoust Soc Am 1986; 80:1007–15.
  
• Baillie C, ed. Green Composites: Polymer Composites and the Environment. CRC, 2005.
  
• Barbero E. Finite Element Analysis of Composite Materials. CRC, 2007.
  
• Bartlett. Materials selection for musical instruments. Proc Inst Acoustics 1997; 19:69-78.
  
• Bartholomew J, Glasser A. Braided composite stringed instrument bow. U.S. Patent 7,262,353. Issued 28-AUG-2007.
  
• Christensen R. Mechanics of Composite Materials. Dover, 2005.
  
• Cremer L. Physics of the Violin. MIT, 1984.
  
• Davidse P, Waterman H, Westerdijk J. Sound velocity and Young's modulus in polyethylene. J Polymer Sci 2003; 59:389-400.
  
• Hinton M, Soden P, Kaddour A-S. Failure Criteria in Fibre-Reinforced-Polymer Composites. Elsevier, 2004.
  
• Horta-Rangel1 J, Brostow W, Martinez-Barrera G, Castaño V. An optimization approach to the computer simulation of composite materials. J Reinforced Plast Comp 2008.
  
• Kaw A. Mechanics of Composite Materials. 2e. CRC, 2005. [see esp. pp. 226ff]
  
• Lagnese J, Leugering G. Controllability of thin elastic beams and plates. In The Control Handbook. William Levine, ed. CRC, 1996. Pp. 1139-56. (Esp. Eq. 66.38)
  
• Leng J, ed. Shape-Memory Polymers and Multifunctional Composites. CRC, 2009.
  
• Matsunaga M, Minato K. Physical and mechanical properties required for violin bow materials II: Comparison of the processing properties and durability between pernambuco and substitutable wood species. J Wood Sci 1998; 44:142-6.
  
• Moon F. Critical survey of wave propagation and impact in composite materials. NASA, 1973. [3MB pdf]
  
• Reinfeld D, Loft A. The Violin Bow. Woodwork, 2000. (DRbows.com)
  
• Rothon R, ed. Particulate-Filled Polymer Composites. Smithers, 2003.
  
• Scott H. Carbon-fiber bows are hot items these days; What’s the right one for you? Strings Magazine 2002; 105.
  
• Sheikh-Ahmad J. Machining of Polymer Composites. Springer, 2008.
  
• Vinson J, Sierakowski R. Behavior of Structures Composed of Composite Materials. 2e. Springer, 2008.
  
• Wegst U. Wood for sound. Am J Botany 2006; 93:1439-48. (esp. p. 1446 on bowsticks) [1MB pdf]
  
• Wetzlinger A, Musing B. Stick for a string instrument bow and processes for its production. U.S. Patent 6,075,188. Issued 13-JUN-2000.
  
• Wilson D, Vinson J. Viscoelastic effects on the buckling response of laminated columns. ASTM Publ. 864. ASTM, 1985.
  
• Xenophontos C, Kurtz J, Fulton S. A p-version MITC finite element method for Reissner–Mindlin plates with curved boundaries. J Comput Appl Math 2006: 192:374-95.
  
• Young D. New frontiers of expression through real-time dynamics measurement of violin bows. Master’s Thesis, MIT, 2001. [1MB pdf]
  
• Zaikov G, Bouchachenko A, Ivanov V, eds. Aging of Polymers, Polymer Blends and Polymer Composites. Nova, 2002.