jwilzewske: Change We Can Believe In: Sofia Gubaidulina’s Mathematics of Physical and Religious Time

Co•na•tiv•i•ty (kō-nā-tiv'-ə-tee)
n. The aspect of mental processes or behavior directed toward change, including impulse, desire, volition, and striving.”

To-date, the analytical attention that’s been paid to Fibonacci series and other mathematical constructs in the compositions of Sofia Gubaidulina (София Асгатовна Губайдулина) has mainly concerned the role of mathematics in devising her melodies and harmonies and in guiding her voice-leading. Actually, it’s unclear whether Sofia actually uses the words ‘numerology’ or ‘gematria’ in discussing her own compositional methods. Her methods are in any case deeply associated with her Russian Orthodox religious beliefs and spiritual practices.

But besides the mathematical origins of her choices of pitches, she also creates ‘ambient’ fields of multi-rate polyrhythms that are based on the recursive Fibonacci and other mathematically derived series. Becomingness. ‘Change we can believe in,’ to borrow a phrase from the just-completed political election process in the U.S. I’ve recently been exploring recordings of Gubaidulina’s compositions, to discover Fibonacci-accelerando and Fibonacci-ritardando patterns—rhythmic counterparts to her number-theory-based polyphony. This CMT post is meant to tell you a little about what I am finding so far.

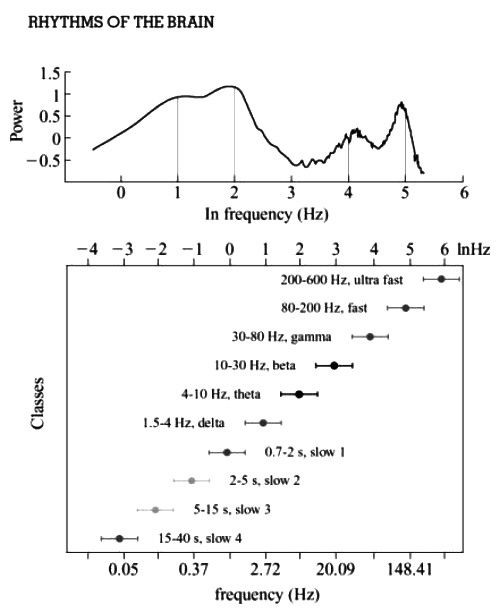
T hree hippocampal rhythms: theta rhythms (4-10 Hz), gamma rhythms (30-80 Hz), and a fast oscillation (140-200 Hz). These rhythms are independently generated; we have observed that gamma oscillations persist without theta and compete with fast oscillation... There is a definable relationship among all brain oscillators: a geometric progression from band to band with a roughly constant ratio of e— the natural (Naperian) logarithm. Since e is an irrational number, the phases of coupled oscillators of the various frequency bands will vary on each cycle forever, resulting in nonrepeating, quasi-periodic, or weakly chaotic pattern: this is the main characteristic of the EEG. [But] why are there so many oscillators [in the brain]? Why can the brain not use a single, fixed-frequency clock for all of its computing functions? There are multiple answers to these questions... Once a slow oscillator appeared in simple animals, faster ones could be added as needed in subsequent evolutionary stages [for controlling functions on faster timescales]. We observe the continued coexistence of all of those independent clocks in the neurophysiology and neuroanatomy of brains today. The brain is not like a single, precise, fast clock and time-division [to produce a series of slower clock rates from the fast master clock] as is seen in digital computers. [‘Intelligent Design’ zealots notwithstanding,] the human brain did not appear de novo. The myriad independent clocks are the residue of evolution of the brain over many millennia. There is extra resilience and survival fitness that comes from the multiplicity of biological clocks, from the N-fold redundancy”
— Gyorgy Buzsaki, Rhythms of the Brain, p. 113.

O nce the hippocampus has been primed by stimuli that come down the perforant pathway, its own subsequent responses are greatly enhanced. Three seconds after granule cells in the hippocampus receive their first priming burst from above, they open up the ‘gates’. They transmit impulses much more efficiently across their synapses. This enhancing effect rises to its peak 15 to 20 seconds later. What is the most effective rate at which to deliver these brief trains of potentiating stimuli? Stimulating at the natural theta frequency: 5-7 Hz. Why is the result called ‘long-term potentiation’? Because transmission remains increased for as long as three weeks after the stimulation. Where does the theta rhythm come from? Chiefly from the medial septal region. Medial septal cells are ‘pacemaker’ cells. Their temporal pattern of acetylcholine release drives theta rhythms throughout the hippocampal formation.”
— James Austin, Zen and the Brain, p. 181.

Since the 1980s Gubaidulina’s work has been deeply informed by her Orthodox faith and her ‘zahlenmystik’, or the use of gematria, numerology, mystical mathematical formulae such as the Fibonacci series and the Golden Ratio. Sofia began to use the Fibonacci sequence as a way of structuring the form of the work. The sequence was especially appealing because it provides a basis for composition while still allowing the form to ‘breathe’—the naturalism referred to above. It plays a prominent role in such pieces as ‘Perception’, ‘Im Anfang war der Rhythmus’, ‘Quasi hoketus’ and the symphony ‘Stimmen... Verstummen...’ ). Later the Lucas series and Evangelist series, sequences derived from that of Fibonacci, were added to her repertoire. These compositional devices and effects are easiest to study in Gubaidulina’s chamber works.

There’s a naturalness ... an innate and almost inevitable quality to Gubaidulina’s rhythmic structures. The proportions of the durations and the statistical distributions of the durations of notes feel like ratios and distributions that we are deeply familiar with from phenomena that occur in Nature. When things ‘wind-up’ toward a climax in a Gubaidulina composition, they wind-up in the manner that we see when gravity accelerates a falling object. When things ‘wind-down’, they wind-down in a progressively diminishing pace that we see in dissipative processes in Nature. The music of Sofia Gubaidulina imparts a distinct impression that it complies with the Laws of Thermodynamics and other physical principles. Mass and Energy are conserved, neither created nor destroyed in the course of performing the music. Entropy increases slightly from the beginning to the end of each piece. It can be measured, if you are inclined to do so. But even if you don’t measure it, you feel it. The Universe is proceeding as it should.

Apart from the Orthodox spirituality that Gubaidulina intended to confer on her compositions, all listeners can at least apprehend the ‘organic’ cosmology that her compositional designs embody—the internal consistency and balanced energy and entropy budgets.

Okay. Measure it? Sure. Take one of her simpler pieces, like ‘Serenade’—the Swedish guitarist Mats Bergström (jpeg above) has a nice recording of this piece. It’s clear and the polyphony and rhythmic complexity are not too daunting. The Gibbs-Shannon entropy of a random variable that takes on values i with probability p_i is defined as:

If the rhythmic lines’ clock-rates are arranged so as to be Poisson-distributed, then the entropy of the Poisson distribution is given in terms of an infinite sum:

where λ is the time-constant of the distribution. For long values of λ, the asymptotic form of this expression is:

Or, in a slightly different formulation, the Renyi entropy of order α where α varies between 0 and 1 is defined as:

Obviously, if a composer sticks scrupulously to a mathematical construct in devising rhythms and orchestration, the result may be too complex to be playable. So there are compromises and simplifying decisions to make—collapsing the complexity into something that retains the feel of the programmatically-generated structure but omits things that inject too much variability or impose cognitive demands that are excessive. There’s a need to write forms that support ‘mutual entrainment’ of the disparate rhythms, re-syncing them on some regular basis. I try computing statistical copulas, to do multivariate measurement of synchronization/association between clocks...

Sofia Gubaidulina, Serenade, Fibonacci-beamed 10:3, 11:3, 12:3

C ommunities of Clocks... ‘Mutual entrainment’ is a theme that recurs again and again throughout the physiology of coupled rhythmic systems... [The systems’] ‘phase-scatter’ is altered in proportion to the derivatives of new clock-phase with the old phase and the magnitude of the perturbing stimulus, as characterized by the following differential equation:
— Arthur Winfree, The Geometry of Biological Time, p. 119.

Winfree, Clock-phase ‘mutual entrainment’ of two coupled biological clocks

Based on my measurements thus far, it looks like Gubaidulina’s ‘Fibonacci N-tuplets’ (? Fib-tuplets) and other rhythmic figures are hard for humans to play in a perfectly Fibonacci-timed way. With the note-durations normalized to the duration in milliseconds of each N-tuplet, the 10:3, 11:3, and 12:3 Fib-tuplets in ‘Serenade’ have as-written theoretical Shannon entropies of -2.06, -1.78, and -1.58, respectively.

As performed by Bergström, we get average values of -2.11, -1.85, and -1.72——entropy values slightly lower (more ‘ordered’) than the theoretical as-written values, owing to the [neurophysiology of entrainment that gives the--] plateauing of durations in the middle. (N-tuplets comprised of notes of perfectly identical durations would have Shannon entropies of -2.30, -2.18, and -2.07, for the 10:3, 11:3, and 12:3, respectively.) Interesting...

The ‘clocks’ in our brain that control our muscle function evidently tend to rush the accelerando beginning and ritardando ending just a little, and have a rate ‘plateau’ in the middle where the durations of the notes do not change as much from note-to-note as they should if they were strict, perfect Fibonacci.

It’s just how we're ‘built’, part of our innate physiology—beyond our interpretive control, really. What Gubaidulina reveals in these Fib-tuplets is a boundary between our humanity and our animality; between our conscious, sapient nature and our unconscious, instinctual nature; between things under our control and things that are beyond the possibility of human mastery. It is a fine and beautiful thing she does, reminding us performers and listeners of these things—we are stewards, not owners, of our mortal, animal bodies; we should be mindful of other animals with whom we share the planet; and so on. The Fib-tuplets induce a rhythmic meditation on humility, a spiritual posture that is receptive to grace... Have a listen to the MP3 clip below and you will see what I mean.

MetanoiaMind.com ‘EEG rhythms and states of consciousness’

And the spiritual effect of these naturalistic, physiologically propelled rhythmic structures is what I would say is this: ‘instantaneous epiphanies’ during neural pulse-entrainment. Maybe not on the first performance or the first casual listening. But if you do these pieces with intensely focused repetition, as part of a meditative practice? Wow! How long does an epiphany take to reach? And, once arrived, how long does the moment last? Try it and see!

So Gubaidulina’s music can induce dramatically altered perceptions of time, and transport the listener or performer to ecstatic, mystical, sufi-like states. Try it when you’re alone with your ‘significant other’. Maybe you will get to some exotic tantric, transfigurational, mutual-entrainment place you’ve never been to before. Change you can believe in! The tantric, ecstatic quality of Gubaidulina’s writing is maybe related to ‘theosis’ or the ‘Doctrine of Deification’ and ‘participatory union’ with God in the orthodox patristic tradition (see Russell, Tatakis, and Zizioulas links below).

Mats Bergström is a graduate of the Royal University College of Music (RCM) in Stockholm and Juilliard in New York. He made his recital debut at the Wigmore Hall in London in 1983 and has since pursued a career as soloist, accompanist and ensemble player in various genres. In 2006, he was elected member of the Royal Swedish Academy of Music. He performs solo recitals as well as the standard works for guitar and orchestra, and collaborates with artists such as singers Malena Ernman, Annika Skoglund, Olle Persson and Mikael Samuelson, flautist Anders Johnhäll and violinist Joakim Svenheden. He stretches the concept of chamber music in much of his work. Beautiful, fascinating. Mats currently lives with his wife and 3 kids in an old schoolhouse 30 km northeast of Uppsala.

[50-sec clip, Mats Bergström; Sofia Gubaidulina, ‘Serenade’, mm. 22-35 1.2MB MP3]

Here is a little spreadsheet I put together, which shows the Fibonacci-prescribed accelerando and ritardando timings for Gubaidulina Fib-tuplets that appear in ‘Serenade’ and other of her compositions. You can click on the screenshot to explore or download a copy to play with. Enjoy!

A student doing a practicum in a nursing home reported to me an incident. She was walking with a resident along the hall where there were pictures of various bucolic, relaxing, unobtrusive scenes. One was a painting of a blacksmith shoeing a horse while a small boy looked on. The patient stopped at this picture and told the student, ‘This is a picture of me and Dad.’ The student asked me if, in fact, the picture was of the resident and his father. I told her that the patient's father had indeed been a farrier and that when he was young the son had often helped his father, but this was merely coincidental. The mid-19^th Century Currier & Ives ‘Village Blacksmith’ picture was certainly not a depiction of this particular man and his father in 1925.”
— Allen Edwards, A Psychology of Orientation: Time Awareness Across the Life Stages and in Dementia, p. 208.

[This moment was for the elderly man ‘epiphanic’. And his fugue-like behaviors and experiences were these days continuously filled with small epiphanies. How brutal it would be to dispute his statement. How utterly awful to try forcibly to ‘correct’ the patient’s ‘mistake’ by compelling him to acknowledge it is Currier & Ives’s picture of some generic blacksmith, as a part of a cruel regime of medicalizing and treating the patient’s ‘confusion’ or ‘disorientation’. The old man’s variant, epiphanic reality must be permitted to stand——must be allowed anyhow if one cares a jot about his psychological condition and spiritual future.
—— dsm.]

jwilzewske

Wednesday, November 5, 2008

Change We Can Believe In: Sofia Gubaidulina’s Mathematics of Physical and Religious Time

No comments:

Post a Comment