jwilzewske: Pražák Fractal Vista Overlook

[I am] “always searching for the meaning of life, searching for truth. A system of uncertainty has entered our daily life. The pressures of mechanization and uniformity to which life is subject call for protest ... by music.” — Bohuslav Martinů.

DSM: Martinů’s String Quartet No. 3 (H. 183, 1929)—performed so beautifully by the Pražák String Quartet this evening—reminds me a lot of Iannis Xenakis’ music. In 1972 at the University of Minnesota I attended lectures given by Xenakis. It was astonishing to me at the time how organic and natural—How expressive!—the structures and textures in this music could be—pieces whose heritage was mathematical, that is. Martinů’s music has this same sort of formal beauty—it has a mathematical beauty.

CMT: Yes, that’s true! As though it were derived from the theory of fractals! Quantitative fractal mathematics analyses of heterophonic ‘webs’ of sound lilke Martinů’s and Shostakovich’s and Xenakis’ string quartets. In fact, there’s a vibrant research literature that addresses the ‘after-the-fact’ mathematical analytics and theory side of it. But, you’re right, the real surprise is that mathematics can guide or produce the composition itself—or major elements of it, the raw materials, or completing or correcting the orchestration. So the mathematics and software don’t just analyze it after the fact. They can generate it and build it. And the deeper surprise is also that wholly ‘stochastically-generated’ pieces can actually signify things to us and move us! At least some of them can. As if there were some Law of the Universe that should make such a thing heretical or cognitively impossible. As if! ‘Stochastic music’ is the name given to the mode of composing music developed by Xenakis and put forward in his classic book “Formalized Music,” first published in France in 1963. Music composed this way isn’t by any means ‘random’ music; instead, it’s musical phrases and textures by mathematical random-walk diffusion, martingales, discrete Brownian motions, mathematical Itô processes. The trajectory of each phrase is related to its immediate predecessor—a Markovian nearest-neighbor regime—which is probably why it does seem organic and cohesive. Each step is sensible and coherent in the context of what just preceded it. And the result exhibits the four musical textures that are recognized on conventional music theory: monophony, homophony, polyphony and heterophony:

Monophonic texture has a single melody or single line of sound;
Homophonic texture is is comprised of a succession of ‘block’ chords;
Polyphonic texture has two more concurrent, independent lines of sound;
Heterophonic texture consists of variant versions of the same musical line played concurrently—a musical ‘braid’.

Martinů’s and Xenakis’ music has such textures, every bit as much as the music of Mozart or Beethoven does!

DSM: As technology improved in the Sixties, computers were an ever more essential tool for Xenakis. Beginning with Achorripsis in 1956, he used software apps that linked musical parameters (timbre, duration, intensity, and so on) via mathematical game-theoretic algorithms. By separating non-temporal parameters (like pitch) from temporal ones (like rhythm) in his algorithms, Xenakis produced intricate constructions—pieces like Tetras (1983), which was dedicated to the Arditti String Quartet.

CMT: You know, I think he was in those days a lightning rod for criticism on this point, because many people misunderstood what he was doing with computers. Or they thought it was somehow reductionistic or devaluing of the human element—or a backhanded denial of transcendence in music. People’s misunderstandings then might be likened to a vehement but spurious objection to the ‘Turing Test’ in computer science or philosophy of Mind. Or Searle’s ‘Chinese Room’. Instead, Xenakis regarded composing as a structured kind of creativity—one governed by rules and variables and, for him, one that could be aided by technology—but still admitting of lots of flexibility with those rules. Xenakis once spoke of the distance separating expression and composition: “...that kind of traditional sentimental effusion of sadness, gaiety or joy—I don’t think that this is really admissible in my music.” Well, today far fewer people raise objections like the ones that Xenakis faced. If you’re a mechanical engineer designing complex systems, you use Parametric Technology Corp’s Pro/E™ software; if you’re a doctor you use things like ePocrates™; if you’re a graphic artist, you use Adobe’s InDesign™ and Illustrator™ and QuarkXpress™ and other things—giclee is not a dirty word—and if you’re a composer you use Coda’s Finale™ and myriad other software packages. You can still compose with rocks and sticks if you want to—nobody’s stopping you. But many today do use some level of technology as part of how they compose these days—and nobody disparages the use of tools per se. Yes, a ‘Fool with a Tool’ is still a Fool. But the tool itself doesn’t produce bad compositions. And the human composer isn’t abdicating or demoting herself/himself to the role of copy-editing what the tool generates. Mere use of machines and algorithms by no means denotes an acceptance of mechanization, or of a bland monoculture! In other words, the Luddites, I think, mostly faded out about twenty years ago or so. A Kuhnian paradigm shift happened somewhere along the line, and now there is pretty alacritous acceptance of what the previous generation had found very threatening. Use of algorithms in composition is no longer sacrilege.

DSM: But the irascibility was surely part of Xenakis’ lectures back in 1972. “Sentimental effusions not admissible in my music!” Or Martinů’s “Mám toho plné zuby!” (I’m fed up!) Basically, he implied that others’ work was excessively sentimental or overwrought or—Horrors!—bound by tradition. But, despite Xenakis’ rants, he wasn’t actually “anti-expressive” as such—not more than Martinů was anyhow. From his wartime experiences (“the agony of my youth, of the Resistance”), Xenakis declared his yearning for the transcendent: “For years I felt guilt at having left the country for which I’d fought. I left my friends. I felt I had a mission. So my thoughts were moving around more general, universal problems. I became convinced that one can achieve universality, not through religion, not through emotions or tradition, but through the sciences.” So, like Martinů, Xenakis’ attention to musical texture and form was not at all “cold”—despite his use of mathematics and despite the computers in his acts of composing. He was a warm, friendly, brilliant guy. Iconoclastic and irascible, yes, but deep-down he was warm.

CMT: What about other types of mathematics in music composition? Wavelet theory? Horizontal (longitudinal) cliques; vertical cliques; signals convolved with other signals! String Quartets Nos. 3, 4, and 5 are examples of Martinů’s mathematically convolving Czech folk music signals with the neo-Classical signals that radiated throughout Europe’s music scene in the pre-War years. These Quartets’re full of diverse sonorities and technical effects; they’ve got rich vertical texture and longitudinal texture. But—Look!—they’re also balancing passionate chromatics and harmonies with the crystalline form and independence of the voices—quintessential quartet writing. Very conversational! As you said, despite his use of formal mathematical techniques, Martinů wrote “[I am] always searching for the meaning of life, humankind's life and my own, searching for truth. I feel the pressure of the contradictory forces, I would like to find a ‘common denominator’ which would absorb these contradictions. [There is a] system of uncertainty that came to our daily life.The pressure of mechanization and uniformity which our life is subject to, [and this] evokes our protest ... in music.” The formalism—the way he composed—was in fact a part of this humanistic protest!

DSM: The No. 3 Quartet is witty—funny, even—this string quartet, written wryly in F major. Martinů was 33—he was young still when he moved from staid Prague to wild Paris in 1923. There is a jaunty, playfulness in the Vivo in this Martinů No. 3—it’s bohemian in the cultural sense of the word, as well as literally bohemian in respect of Martinů’s ethnicity. Yes, this quartet was clearly composed to please Martinů’s intended avant garde listener. But the Quartet’s disciplined part-writing gives each of the four voices a unique identity. This Quartet rewards the audience for a close listening. But if listeners aren’t attentive enough, they’ll merely be annoyed.

CMT: The independence of these lines makes for some major dissonant clashes with each other. In the outer movements these gestures produce effects that, to me, are humorous, but there’s a tragic quality in the middle movement. The violin seems to lift the whole texture into higher registers, and the music takes on a more driving character as the percussive effects become more prominent.

DSM: True. And these disturbed chords and low trills add a darkness that ascends to the climactic central section and resolves in a mood of resignation—and acceptance. Extravagant, prodigal, cavalier, epicurean.

CMT: The second quartet, with its direct impressionistic influence, is even more “profligate” in its tone and range of innovative textures and flavors. It implies a composer who is all-seeing, detached-but-interested—the perspective of an observer at a distance, one who has no immediate sense of his mortality—a young person’s view from a belltower or belfry, rather than from ground level. Martinů spent the first twelve years of his life looking at his village from this bird’s-eye perspective, you know. His father was the local carilloneur. The memory of this view of the world, experienced every week with his father, was inscribed upon the young Bohuslav’s mind—how could it not but influence his ideas of composition! As he wrote later in life, it was “not the small interests of people, the cares, the hurts, or the joys” that he saw from that great height, but “space, which I always have in front of me.”

DSM: At Martinů’s funeral, the eulogist characterized Martinů's work by saying, “His music is the music of our times, because it expresses profound basic problems; it bears the stamp of individuality, which enables it to ring out among all the rest, and guarantees that he will not be forgotten.”

CMT: During 2007, quite a few North American audiences will be fortunate to hear the Pražák String Quartet—including New York, Boston, Houston, San Francisco, Los Angeles, Detroit, New Orleans, Salt Lake City, Tucson, Vancouver, and Montreal. Pražák’s Kansas City performance tonight was just an appetizer!

Here are some tasty “morsels” for you:

and these too:

DSM: Šťastnou cestu! (Have a good trip!)

CMT: Děkuji! (Thank you!)

DSM: Prosím! (You’re welcome!)

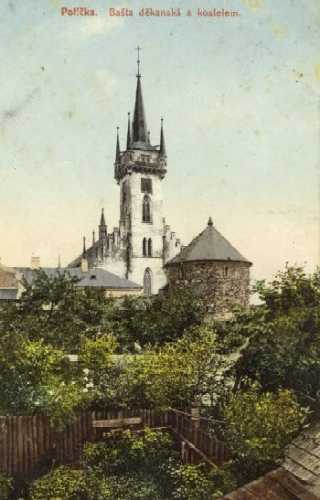
Martinů’s Boyhood Vista, Polička, 100 mi east of Prague

jwilzewske

Friday, November 3, 2006

Pražák Fractal Vista Overlook

No comments:

Post a Comment